CONJETURA DE COLLATZ
Actualizado 16 de Marzo de 2023por Eduardo Saenz de Cabezon, por el canal DERIVANDO
Conjetura de COLLATZ
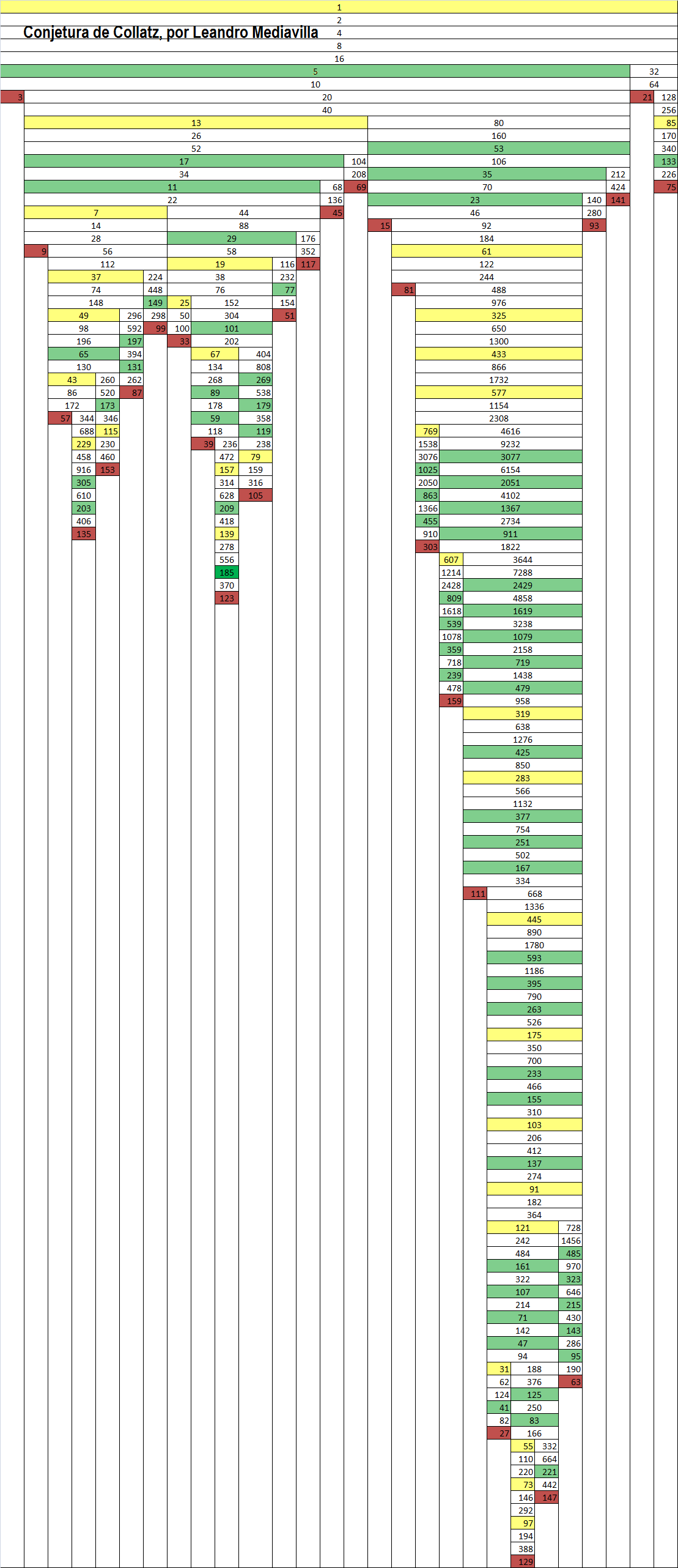
Imagen 1
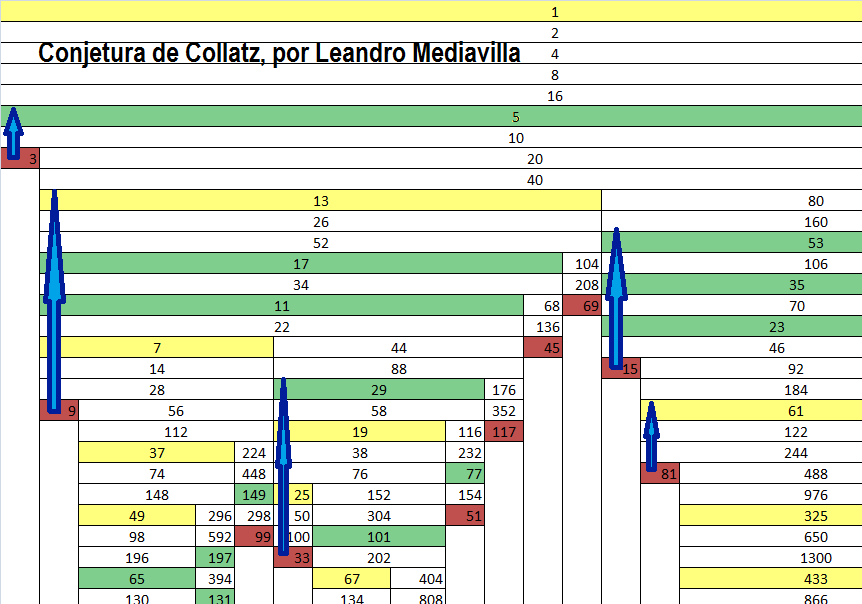
Es el desarrollo de la Conjetura de Collatz en la forma clasica de arbol, iniciando desde el numero 1.
Aplicando la inversa de la conjetura de Collatz, voy avanzando y en cada paso ingreso el o los numeros que van apareciendo.
Cuando en un paso hay dos resultados posibles, el numero impar lo pongo del lado izquierdo de la hoja y el numero par del lado derecho.
Continuo hasta el paso 16, aplicando la Inversa de Collatz a cada numero que va apareciendo.
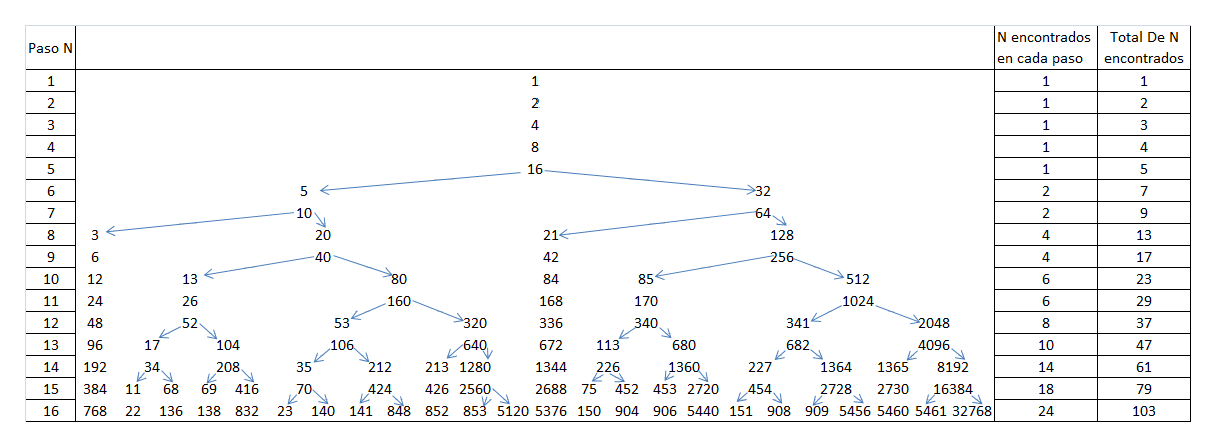
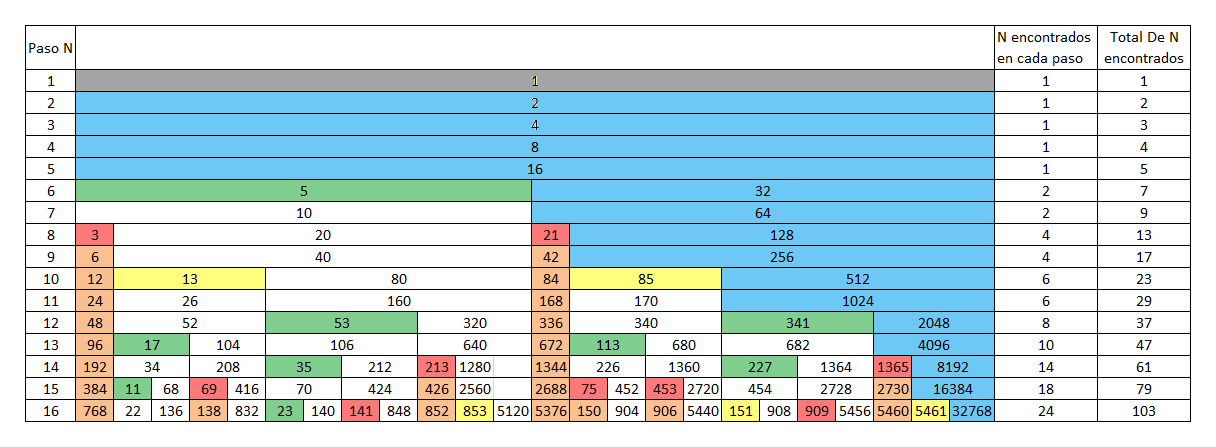
Imagen 2
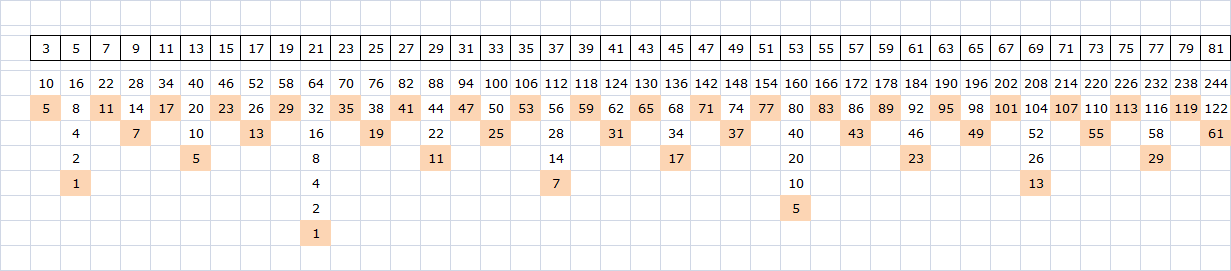
Es el desarrollo de el mismo arbol de la Imagen 1, pero convertido en una tabla ordenada.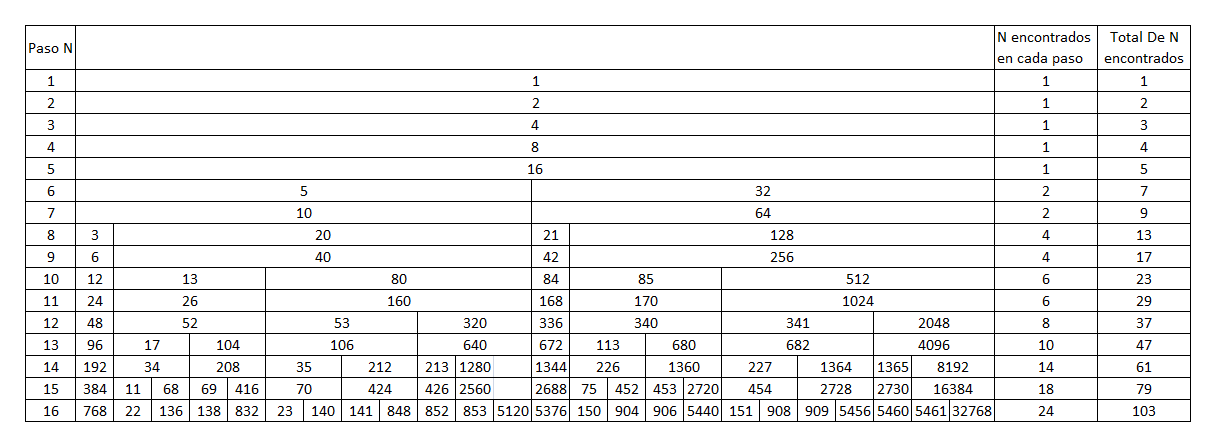
Imagen 3
Voy clasificando la tabla por colores. para buscar patrones.A los numeros pares, les pinto el fondo de color blanco.
A los numeros impares, les pinto el fondo de color gris.
A las potencias de 2, les pinto el fondo de color celeste.
Las potencias de 2 siempre va a ser el numero mayor de cada paso.
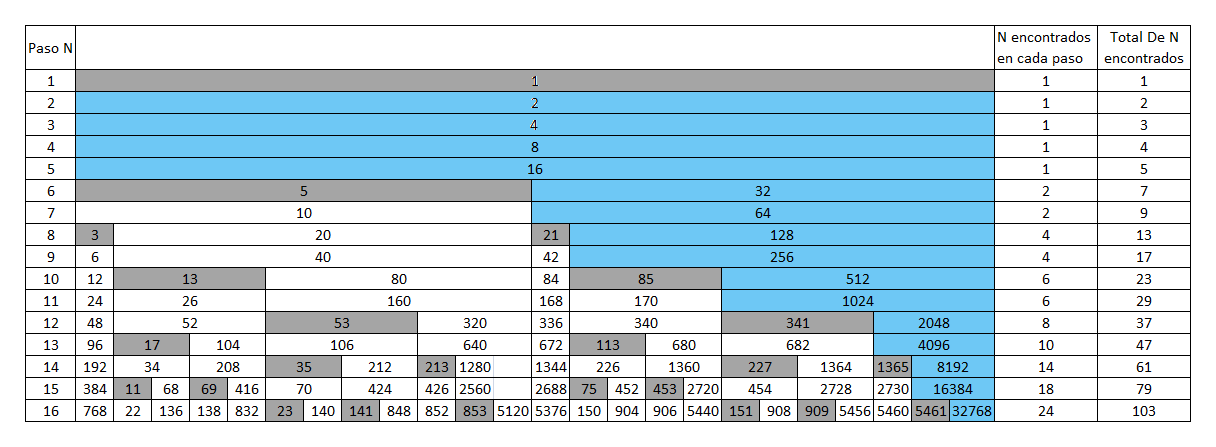
Imagen 4
Se van formando escaleras imaginarias que descienden, cada escalera imaginaria desciende infinitos escalones.
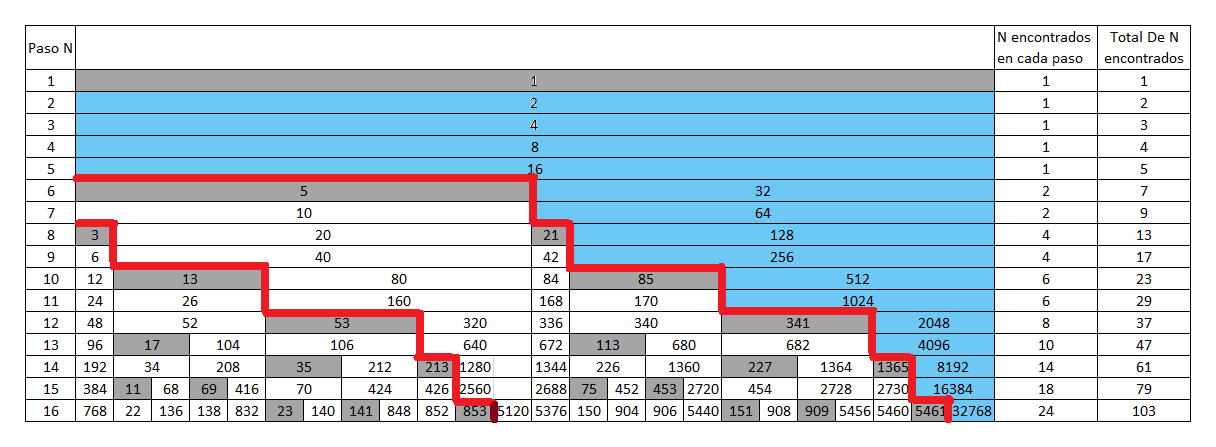
Ejemplo: En el paso 8, la escalera la incia en el Nro 3, y los escalones son 3*4+1=13, 13*4+1=53, etc.
Si empezamos a aplicar la conjetura a los numeros 3, 13, 53, 213, etc. El proximo numero impar que hay arriba de ellos, va ser para todos los casos el numero 5.
Si tenemos en cuenta solo los numeros impares, arriba de cada escalon de una misma escalera, se encunetra el mismo numero impar.
Esto sucede en cada escalera.
Imagen 5
Clasifico los numeros impares en 3 grupos.
De colores rojos, amarillos y verdes.
Fondo color rojo: Son todos los numeros impares divisibles por 3.
Los numeros que al dividir por 3, de de resto 0.
Como el numero 3, 9, 15, 21,etc.
A partir de un numero impar de color rojo, cada vez que apliquemos la inversa de Collatz encontramos unicamente numeros PARES divisibles por 3 y nunca mas aparecera algun numero IMPAR.
A estos numeros pares devisibles por 3, los coloreo de color anaranjado para identificarlos.
Fondo color amarillo: Son algunos numeros impares NO divisibles por 3.
Son los numeros que al dividir por 3, de de resto 1.
Como el numero 7, 13, 19, 25, 85, 151, etc.
A partir de un numero impar de color amarillo, cada vez que apliquemos la inversa de Collatz, encontraremos 2 pasos con numeros pares, y al tercer paso aparecera un numero Impar, que puede ser rojo, verde o amarillo.
Fondo color verde: Son algunos numeros impares NO divisibles por 3.
Son los numeros que al dividir por 3, de de resto 2.
Como el numero 5, 11, 17, 53, etc.
A partir de un numero impar de color verde, cada vez que apliquemos la inversa de Collatz, encontraremos 1 solo con un numero par, y en el segundo paso aparecera un numero Impar, que puede ser rojo, verde o amarillo.
Fondo color anaranjado: Son todos los numeros pares divisibles por 3.
Estos aparecen debajo de los numeros Impares de color rojo y debajo de otro numero anaranjado.
El orden de Colores que van apareciendo en una escalera imaginaria es siclico (Amarillo, verde y Rojo)
Imagen 6
Clasificamos a los bordes de los numero impares en dos grupos, bordes verdes y azules.
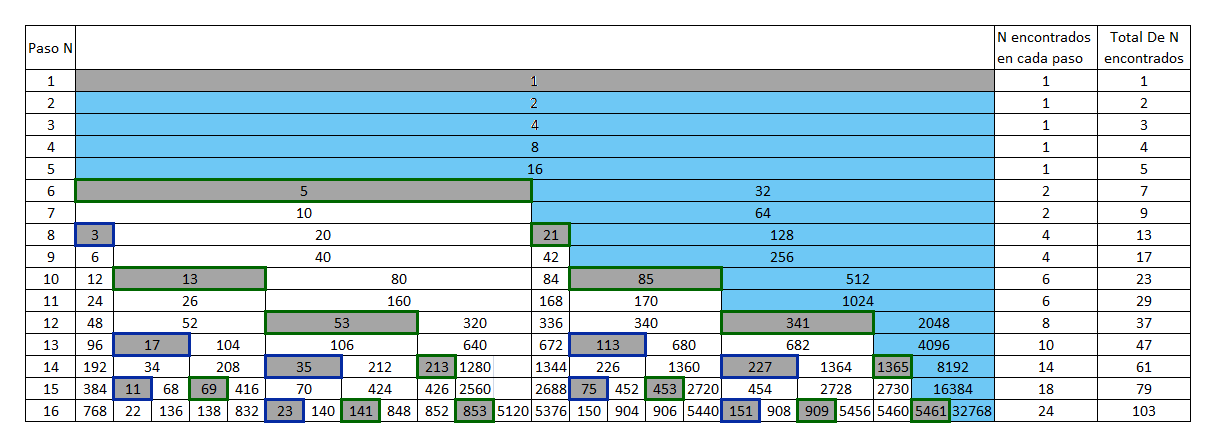
Borde azul: Al primer escalon, que inica una escalera imaginaria.
Pinto los bordes de color azul, a los numeros impares que, al aplicar (x-1)/4 de como resultado, un numero que NO sea, un numero impar entero.
Ej: 3 por que (3-1)/4=0.5 - No es un numero impar entero,
23 por que (23-1)/4= 5.5 - No es un numero impar entero,
113 por que (113-1)/4= 28 - No es un numero impar entero,
Borde verde oscuro: A todos los escalones, que NO inican una escalera imaginaria, y ya forman parte de una.
Pinto los bordes de color verde, a los numeros impares que, al aplicar (x-1)/4 de como resultado, un numero que SEA, un numero impar entero.
Ej: 5 por que (5-1)/4= - Es un numero impar entero,
13 por que (13-1)/4= 3 - Es un numero impar entero.
21 por que (21-1)/4= 5 - Es un numero impar entero,
Al lado de un escalon X de Borde verde oscuro, siempre va a estar a su izquierda X-1 (menos en el numero 5)
Ej: Paso numero 8, numeros 20 y 21 (21 borde verde oscuro),
paso numero 10, numeros 12 y 13 (13 borde verde oscuro),
paso numero 16, numeros 140 y 141 (141 borde verde oscuro),
Imagen 7
Es la suma de la imagen5 y la imagen6.
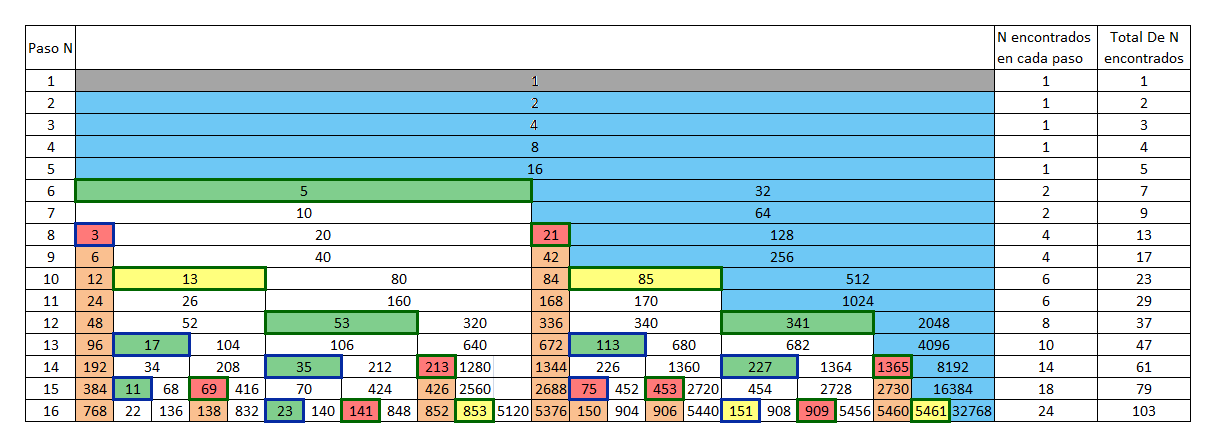
Primeros 23 Pasos de la conjetura de Collatz,
Click en la img para agrandar.
Imagen 8

Numeros impares del 1 al 100 dentro de la conjetura de Collatz,
Click en la img para agrandar.
Imagen 9
Para continuar es fundamental tener incorporados los conceptos de colores y bordes mencianados hasta el momento.
Todas las personas que se enfrentan a la conjetura de Collatz, empiezan a buscar patrones del siguiente modo.
Imagen 10
Pero despues de años de pruevas, de llegar al mismo lugar que llegaron otros y no tener nada en concreto, abandone este motodo.
Apoyandonos con la Imagen 9, vemos que los numeros impares que no son divisibles por 3 (escalones fondo verdes y amarillos), forman una cadenas de numeros impares que se generan siempre a partir de un numero impar divisible por 3 (escalones fondo Rojo). recordemos que debajo de los escalones rojo hay solo escalones naranja y nunca mas aparecen numeros imapres
Desarrolamos el mismo listado de la Imagen 10, pero aplicando la inversa de Collatz, para tratar de comprobar si todos los numeros impares inician desde un multiplo de 3.
Imagen 11

La Linea inicial queda con un patron horizontal de 3 colores.
| Rojo | Verde | Amari |
Partiendo desde este nivel incial y desarrolando la Inversa de Collatz, para repetir el patron horizontal de color, hay que sumarle 6 a cada numero.
Ejemplo:
| 5 | +6 | 11 | +6 | 17 |
Imagen 12

| x | Rojo | Rojo | x | Amari | Verde | x | Verde | Amari |
Al segundo patron se llega despues de desarrolar 3 veces el patron del nivel superior
| Rojo | Verde | Amari | Rojo | Verde | Amari | Rojo | Verde | Amari |
Pero con la siguiente particularidad...
Debajo de cada uno de los numeros amarilos, aparese 1 numero Rojo, 1 Amarillo y 1 Verde
| Rojo | Verde | Amari | Rojo | Verde | Amari | Rojo | Verde | Amari |
| Rojo | Verde | Amari |
Debajo de cada uno de los numeros Verde, aparese tambien 1 numero Rojo, 1 Verde y 1 Amarillo
| Rojo | Verde | Amari | Rojo | Verde | Amari | Rojo | Verde | Amari |
| Rojo | Amari | Verde |
Por logica debajo de las 3 veces que aparece el numero de color Rojo, no se encuentra ningun numero Impar
Quedando este segundo patron con 6 numeros,2 Rojos 2 verdes y 2 Amarillos. El doble de numero del patron inicial.
Partiendo desde el nivel incial, para repetir el patron vertical de 2 colores, hay que sumarle 18 a cada numero inicial.
Ejemplo:
| 11 | +18 | 29 | +18 | 47 | +18 | 65 |
| 7 | 19 | 31 | 43 |
Imagen 13

Con la misma logica de la Imagen 12. Cada vez que se repiten 3 Patrones del nivel superior, y se desarrolla la inversa de la conjetura de Collatz, en la siguiente linea se forma un nuevo patron horizontal, que se repite en este nuevo escalon hasta el infinito.
Con la misma logica de antes, cuando haya un numero color verde o amarillo dentro del patron que se repite 3 veces y desarrolle la Inversa de la conjetura, estos nuevos numeros generados van a tomar un color distinto, entre Rojo, Verde y Amarillo (sin seguir una lagica u orden)
Para graficarlo, usamos el ejemplo de la imagen anterior .
| 11 | +18 | 29 | +18 | 47 |
| 7 | 19 | 31 | ||
| 9 | 25 | 41 |
Para que se repita el patron vertical de 3 colores hay que sumarle 54 a cada numero.
| 11 | +54 | 65 | +54 | 119 |
| 7 | 43 | 79 | ||
| 9 | 57 | 105 |
Imagen 14

Quedando este Cuarto patron horizontal con el doble de numero del paso anterior, 24. 8 Rojos 8 verdes y 8 Amarillos.y asi sucesivamente.
Continuando con esta logica, aplicando la inversa de Collatz, vemos que aparentemente todos los numeros verdes y amarillos llegan hasta algun numero de color rojo (impares divisibles por 3), que son los numeros que generan a los demas numeros.

Como varios numeros iniciales verdes y amarillos, llegaban a un mismo numero rojo, repitiendose varios de estos entre medio, buscamos al numero verde o amarillo que abarque a todos los demas numeros hasta llegar al numero rojo.
Para esto, aplicamos a los numeros iniciales los bordes aplicados en la Imagen 6. Bordes azules para los numeros generadores de escaleras, bordes Verdes, para los escalones de las escaleras.
Imagen 15

Imagen 16

Eliminamos todos los numeros iniciales borde azul, dejando solo los numeros bordes verdes, que tienen dentro de su desarrolo a todos los numeros berdes azul.
Imagen 17

Estos Modulos, son magicos, todos los Modulos juntos tienen dentro de su Interior a todos los nuneros impares, y ninguno se repite.
Cada modulo inicia con numero Borde Verde, y termina con un numero de color Rojo, (puede darse el caso que sea el mismo numero para los dos casos, ej el numero 21)
Si obserban la imagen 17, se observan los mismos paterones que vimos a partir de la magen 12, En la primera linea se genera un patron de 3 numeros, 1 numero de cada color, cada 3 secuencia de patrones se genera en la linea de abajo un nuevo patron de 6 numeros.y en la linea de abajo un patron de 12, y asi sucesivamente.
Estos MODULOS, son los que nos dan la pauta que en la conjetura de Collatz, el unico Bucle que existe es el de 4,2,1.
Descripcion y patron de los modulos.
Para que se repita cada Modulo de colores...El numero inicial que es el de borde Verde.
Incrementan 24*3^(cantidad de numeros del modulo -1)
El numero final de color rojo,
incrementan 24 * 2^(cantidad de numeros del modulo -1) * 2^(num amarillos del modulo)
Modulo de 1 numero (1 caso) Incrementan cada 24 num (24*3^0)
Rojo.
| 21 | +24 | 45 | +24 | 69 |
Modulo de 2 numeros (2 casos)
El numero inicial borde verde, incrementan cada 72 num (24*3^1)
verde-rojo
| 5 | +72 | 77 | +72 | 149 | |
| 3 | +48 | 51 | +48 | 99 | +48=24*2^1(num del modulo-1)*2^0(amarillos) |
amarillo-rojo
| 61 | +72 | 133 | +72 | 205 | |
| 81 | +96 | 177 | +96 | 273 | +96=24*2^1(num del modulo-1)*2^1(amarillos) |
Modulo de 3 numeros (4 casos) Incrementa cada 216 num (24*3^2)
amarillo-amarillo-rojo
| 181 | +216 | 397 | +216 | 613 | |
| 241 | 529 | 817 | |||
| 321 | +384 | 705 | +384 | 1089 | +384=24*2^2(num del modulo-1)*2^2(amarillos) |
verde-amarillo-rojo
| 173 | +216 | 389 | +216 | 605 | |
| 115 | 259 | 403 | |||
| 153 | +192 | 345 | +192 | 537 | +192=24*2^2(num del modulo-1)*2^1(amarillos) |
amarillo-verde-rojo
| 85 | +216 | 301 | +216 | 517 | |
| 113 | 401 | 689 | |||
| 75 | +192 | 267 | +192 | 459 | +192=24*2^2(num del modulo-1)*2^1(amarillos) |
verde-verde-rojo
| 197 | +216 | 413 | +216 | 629 | |
| 131 | 275 | 419 | |||
| 87 | +96 | 183 | +96 | 279 | +96=24*2^2(num del modulo-1)*2^0(amarillos) |
Modulo de 4 numeros (8 casos) Incrementa cada 648 num (24*3^3)
| AAAR | AAVR | AVAR | VAAR | VVAR | VAVR | AVVR | VVVR | ||||||||
| 541 | +648 | 469 | +648 | 373 | +648 | 29 | +648 | 341 | +648 | 533 | +648 | 229 | +648 | 53 | +648 |
| 721 | 625 | 497 | 19 | 227 | 355 | 305 | 35 | ||||||||
| 961 | 833 | 331 | 25 | 151 | 473 | 203 | 23 | ||||||||
| 1281 | +1536 | 555 | +768 | 441 | +768 | 33 | +768 | 201 | +384 | 315 | +384 | 135 | +384 | 15 | +192 |
Modulo de 5 numeros (16 casos - 2^4) Incrementa cada 1944 num (24*3^4)
Modulo de 6 numeros (32 casos - 2^5) Incrementa cada 5836 num (24*3^5)
Modulo de 7 numeros (64 casos - 2^6) Incrementa cada 17496 num (24*3^6)
y asi sucecivamente...
Modulo de 18 numeros (131072 casos - 2^17) Incrementa cada 3099363912 num (24*3^17)
| 445 | 593 | 395 | 263 | 175 | 233 | 155 | 103 | 137 | 91 | 121 | 161 | 107 | 71 | 47 | 31 | 41 | 27 |
Este es un ejemplo de los 131072 casos del Modulo de 18 numeros, pero es muy conocido
Este modulo se repite recien con el numero 3099364357 color amarillo borde verde, y concluye en el 201326619 color rojo
Cada vez que elijo un numero Nº y realizo la conjetura de Collatz, va a recorrer los numeros de algun modulo sin repetir ninguno hasta llegar a un numero borde verde (que es un escalon que no inicia una escalera), el numero siguiente luego de encontrar ese escalon borde verde, tampoco se va a repetir, porque este numero va ser parte de otro modulo.
Y como dijimos en la imagen 17, Todos los Modulos juntos tienen dentro de su Interior a todos los nuneros impares, y ninguno se repite. por ese mismo motivo no existe otro bucle que el 4 2 1.. El unico numero impar que esta fuera de un MODULO y que no tiene un numero rojo que lo genere es el numero 1, color amarillo borde azul.